Conebeam CT of the Head and Neck, Part 1: Physical Principles

1. A.C. Miracle a and
2. S.K. Mukherjia,b,c

 

1. ^aDepartment of Radiology, University of Michigan Health System, University Hospital, Ann Arbor, Mich
2. ^bDepartment of Otolaryngology, University of Michigan Health System, University Hospital, Ann Arbor, Mich
3. ^cDepartment of Radiation Oncology, University of Michigan Health System, University Hospital, Ann Arbor, Mich

1. Please address correspondence to Aaron Miracle, University of Michigan Medical Center, Department of Radiology, B2B311 UH SPC 5030, 1500 East Medical Center Dr, Ann Arbor, MI 48109-5030; e-mail: amiracle@med.umich.edu

 

Abstract

 

 

SUMMARY: Conebeam x-ray CT (CBCT) is a developing imaging technique designed to provide relatively low-dose high-spatial-resolution visualization of high-contrast structures in the head and neck and other anatomic areas. This first installment in a 2-part review will address the physical principles underlying CBCT imaging as it is used in dedicated head and neck scanners. Concepts related to CBCT acquisition geometry, flat panel detection, and image quality will be explored in detail. Particular emphasis will be placed on technical limitations to low-contrast detectability and radiation dose. Proposed methods of x-ray scatter reduction will also be discussed.

Conebeam x-ray CT (CBCT) is a relatively recent installment in the growing inventory of clinical CT technologies. Although the first prototype clinical CBCT scanner was adapted for angiographic applications in 1982, the emergence of commercial CBCT scanners was delayed for more than a decade.¹ The arrival of marketable scanners in the last 10 years has been, in part, facilitated by parallel advancements in flat panel detector (FPD) technology, improved computing power, and the relatively low power requirements of the x-ray tubes used in CBCT. These advancements have allowed CBCT scanners to be sufficiently inexpensive and compact for operation in office-based head and neck as well as dental imaging applications. These systems are distinguished by a conical x-ray beam geometry and the use of 3D reconstruction algorithms; most recent models are also fit with FPDs. As they are employed for specific imaging tasks in restricted anatomic regions such as the head and neck, preliminary research suggests that they can produce images with high isotropic spatial resolution while delivering a relatively low patient dose. This first part in a series of 2 articles will review the physical principles underlying CBCT as it is employed in head and neck diagnostic imaging. C-arm CBCT systems used in the interventional suite and CBCT systems used in radiation therapy have been the subject of other reviews.^2–4 Although there are numerous differences between CBCT and conventional fan-beam CT techniques, many of the fundamental physical concepts are the same.

Fundamental Principles of CT

The original clinical CT scanner was introduced by Sir Godfrey N. Hounsfield in 1967. Data acquisition was based on a translate-rotate parallel-beam geometry wherein pencil beams of x-rays were directed at a detector opposite the source and the transmitted intensity of photons incident on the detector was measured. The gantry would then both translate and rotate to capture x-ray attenuation data systematically from multiple points and angles.⁵ Although x-ray sources, acquisition geometries, and detectors have rapidly evolved since Hounsfield's original scanner, the theory behind CT has not changed.

The attenuation of a monochromatic x-ray beam through a homogeneous object is described by the Lambert-Beer law:

where I is the transmitted photon intensity, I_o is the original intensity, x is the length of the x-ray path through the object, and μ is the linear attenuation coefficient of the material traversed. This expression changes for inhomogeneous materials such as human tissue:

Line integrals of the linear attenuation coefficients, μ, can be obtained by taking the negative logarithm of the above expression. A line integral at angle θ through the object is the ray sum, a set of which at a given θ constitutes a projection. The computational problem in CT is to determine μ at a given point from a large set of projections obtained at varying θ about the object, a computation based on the theory formulated by Radon in 1917.⁶

Data acquisition in conventional CT imaging has evolved through 4 generations of acquisition geometries. First-generation scanners used parallel pencil beams of x-rays and required both translation and rotation of the source and a single-detector apparatus. Second-generation scanners introduced fan-beam x-ray geometry and used a single-detector linear array. In third-generation scanners, the single-detector arc was introduced in conjunction with fan-beam x-ray geometry. Fourth-generation scanners used a fan-beam of x-rays and a circular detector array. In current practice, multidetector helical CT (MDCT) scanning is most frequently used, answering the call for reduced acquisition times. MDCT is loosely based on third-generation geometry, though the detector array has multiple rows of detectors.

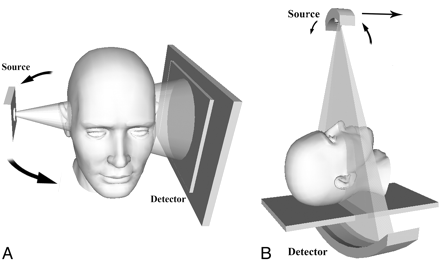
The discussion below will highlight the physical principles underlying CBCT as they contrast with conventional MDCT. A commercially available CBCT system designed for point-of-service head and neck diagnostic imaging will be used as an example (MiniCAT; Xoran Technologies, Ann Arbor, Mich). This system is depicted in Fig 1. Similar systems for office-based dentomaxillofacial applications have been available since 2001.⁷

Data Acquisition

In CBCT systems, the x-ray beam forms a conical geometry between the source (apex) and the detector (base) (Fig 2). This is in contrast to conventional fan-beam geometry (Fig 2), in which the collimator restricts the x-ray beam to approximately 2D geometry. In a fan-beam single-detector arc geometry, data acquisition requires both rotation and z-direction translation of the gantry to eventually construct an image set composed of multiple axial sections. In CBCT systems using a 2D FPD, however, an entire volumetric dataset can be acquired with a single rotation of the gantry. Incident photons on multiple-row detectors in MDCT actually fall on a 2D area of detectors, as with flat-panel detection; indeed, with increasing numbers of rows in MDCT detector arrays, the acquisition geometry actually approximates that of a conebeam system.

A. Cone beam.    B. Fan Beam

FPDs

Digital FPDs enable the direct conversion of x-ray energy into a digital signal with high spatial resolution. The fundamental design consists of a screen of scintillator crystals grown onto a matrix of photodiodes embedded in a solid-state amorphous silicon (aSi:H) or selenium layer. Incident x-rays are photochemically converted to light by the scintillator film and transmitted directly to the photodiode array where the signal-intensity charge is stored. Thin-film transistors fabricated into the aSi:H matrix relay a signal intensity proportional to the stored charge in the photodiode array, which is, in turn, proportional to the incident photons on the scintillator layer. The FPD used in the MiniCAT is an indirect-conversion system based on a cesium iodide (CsI) scintillator embedded in an aSi:H layer. CsI scintillators produce superior spatial resolution owing to the microscopic columnar structure of the CsI substrate, which serves essentially as a fiber-optic conductor for the signal intensity being transmitted to the photodiode array.⁸ FPD arrays afford greater spatial resolving potential with similar noise intensity when compared with their x-ray intensifier/charge-coupled device (CCD) predecessors.⁹

Reconstruction Algorithms

Reconstruction algorithms in tomographic imaging are concerned with producing multidimensional images through the inversion of 1D projection data. The reconstruction algorithm most frequently used in CBCT is a modified Feldkamp algorithm.⁸ The Feldkamp algorithm is essentially a 3D adaptation of the filtered backprojection method used in fan-beam 2D reconstructions.^10,11 The process of filtering, or convolution, involves applying a kernel, or mathematic filter, to raw projection data before it is backprojected. Filtering reduces the blur otherwise inherent in the process of backprojection. The early Feldkamp algorithms solved the inversion problem for acquisition involving full circular rotation of the conebeam vertex about the object. More recent algorithms have been adapted for short circular arc trajectories of the x-ray source.¹²

A primary teleologic difference between CBCT and MDCT is the isotropic nature of acquisition and reconstruction in conebeam systems. In a CBCT system with 2048 × 1536 detector elements—similar to the 1920 × 1536 elements in the MiniCAT detector—for example, reconstruction produces a volumetric dataset with isometric voxels as small as 150 × 150 × 150 μm³ at the isocenter.^2,8 Images can then be constructed in any plane with high fidelity (Fig 3). MDCT reconstruction produces individual sections, which are then stacked. Compared with MDCT, in which 500 × 500 μm² in-plane and 500- to 1000-μm z-axis resolutions are expected, CBCT theoretically reduces the effect of partial volume averaging¹³ and can improve the spatial resolution of high-contrast structures in any chosen viewing plane.

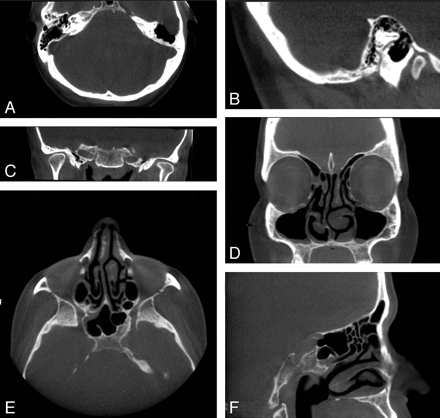Fig 3. Clinical images of 2 patients acquired with the MiniCAT dedicated head and neck CBCT scanner. A−C, Axial, sagittal, and coronal images, respectively, of a patient's normal temporal bones acquired with a temporal bone protocol (40 seconds, 600 frames, 0.3-mm pixels, 125 kVp, 50.85 mA). Voxels are isometric, allowing reconstruction with equally high fidelity in the 3 depicted planes. D−F, Coronal, axial, and sagittal images, respectively, of the paranasal sinuses of a patient with mild mucosal thickenings. These images are acquired with a sinus protocol (40 seconds, 600 frames, 0.4-mm pixels, 120 kVp, 48 mA).

Image Quality

Several physical descriptors and parameters are commonly enlisted to characterize the quality of an image. In characterizing CT systems, quantum noise, spatial resolution, contrast resolution, and detector quantum efficiency (DQE) are of particular interest. Quantum noise is fundamentally related to image quality and is a function of dose, tissue transmissivity, and voxel size. Noise is, in turn, a principal determinant of contrast resolution and, to a lesser extent, spatial resolution, which, along with artifacts, constitute the major observable determinants of overall image quality. CBCT imaging with FPD technology typically affords excellent spatial resolution with a relatively low patient dose. Contrast resolution suffers, however, due to increased x-ray scatter and the reduced temporal resolution and dynamic range of the FPDs.² The discussion below will highlight the physical characteristics relevant to CBCT imaging and the extent to which they impinge on image quality. Scatter will be addressed in detail due to its particular impact on contrast resolution. Dynamic range and temporal resolution will also be addressed in addition to several proposed approaches to improvements in CBCT image quality.

Scatter

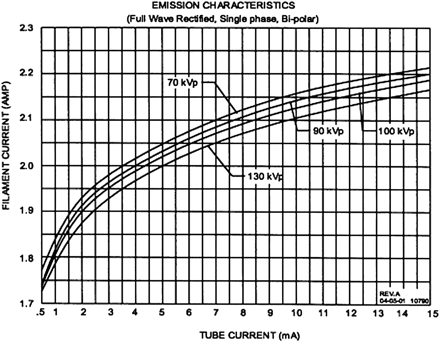
Increased x-ray scatter represents one of the primary technical obstacles in CBCT imaging, limiting image quality in comparison with MDCT. Scatter refers to the off-axis low-energy radiation that is generated in the patient during image acquisition. It corresponds to the contribution to photon fluence at the detector not attributable to the incident primary beam. In conventional fan-beam MDCT, collimation at the x-ray source restricts the z-axis coverage of the beam, only allowing scatter from a thin axial volume of tissue to reach the detector elements during section acquisition. In contrast, CBCT expands the z-axis coverage of the beam, allowing x-ray scatter generated from the entire volume of coverage to reach the detector elements as the image is acquired. The emission characteristics of the MiniCAT x-ray source are depicted in Figure 4.

Scatter contribution is expressed as the scatter-to-primary ratio (SPR) and can be as high as 3 in large-volume CBCT systems compared with ∼0.2 in conventional MDCT systems.¹⁴ Increased scatter not only amplifies patient dose but is a principal contributor to reduced contrast resolution and increased noise in CBCT images. Streak and cupping artifacts (lower voxel values at the image center) can also be produced, further degrading image quality.¹⁵ In an effort to improve the contrast-to-noise ratio (CNR) and reduce image artifacts, multiple approaches to scatter reduction have been investigated and will be discussed below (Fig 5).

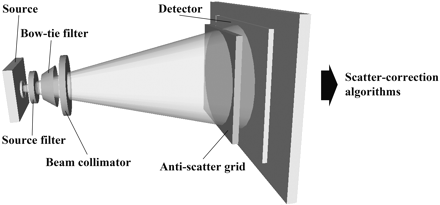Schematic depiction of the methods for reducing and subtracting x-ray scatter from total photon fluence at the detector. Methods are depicted in a series and include source filtration, compensating filtration (bow tie filter), beam collimation, antiscatter grids, and scatter-subtraction preprocessing algorithms.

The modifiable contributors to scatter generation are the imaging geometry (intervening air space or air gap), the z-direction coverage in the field of view (FOVz), and the energy profile of the x-ray beam.¹⁶ To this end, the most basic approaches to scatter reduction are to minimize the FOVz, maximize the air gap, and optimally collimate and modulate the x-ray beam. Unfortunately, FOVz and air gap are dependent on the tissue volume of interest and the spatial limitations of the system gantry, respectively, and, thus, are limited in their ability to minimize scatter. That said, it is still important to select the smallest FOVz possible while continuing to provide adequate target-tissue coverage. Spatial restrictions limit the practicality of further increasing the air gap to reduce scatter, especially in office-based head and neck scanners designed to be compact.

Collimation and Source Filtration

X-ray filtration at the source, beam collimation, and compensating filtration constitute direct methods of scatter reduction. Filtration at the source can be achieved by applying an aluminum filter to remove low-energy photons uniformly from the x-ray beam. Beam collimation eliminates photons outside the intended FOVz, reducing the contribution of peripheral scatter to the SPR in the FOV.⁸

Compensating Filtration

The x-ray path length through tissue at the edges of the FOV is typically shortened in relation to the structure of the scanned object. This results in less attenuation of peripheral scatter and, thus, disproportionately increased peripheral scatter contribution to image degradation. Peripheral scatter not only constitutes the largest contribution to total scatter but forms the basis of the cupping artifact, the effect of which can be mitigated by compensating filtration.¹⁵ The bow tie or wedge filter is the prototypical compensating filter used in CBCT systems. It modulates the beam profile by increasing photon density at the center of the cone and decrementally reducing density at the periphery. In the radiation therapy CBCT literature, Graham et al¹⁵ were able to demonstrate a >50% reduction in scatter with the implementation of copper bow tie filters. Image-quality improvement has been described with bow tie filters in a CBCT system integrated into the gantry of a conventional CT scanner as well.⁸ Compensating filtration is not without criticism, however, because beam hardness has been shown to negatively impact detector efficiency, as demonstrated by a decrease in the ratio of the output signal intensity–to-noise ratio (SNR) to the entrance exposure (SNR/entrance exposure).¹⁷ The kilovolt (peak) (kVp), which is related to the beam hardness, has also been shown to produce optimal low-contrast detectability when it is kept at lower settings.¹⁸ Thus, although scatter and cupping artifacts may be reduced with bow tie filters, this reduction may come at the expense of detector efficiency and low-contrast detectability.

Compensating filtration and the other direct scatter-reduction methods at the source side of the apparatus have the added appeal of reducing patient dose and can, of course, be used in series.⁸

Antiscatter Grids

Antiscatter grids represent an alternative method of direct scatter reduction that has been used with FPDs in digital radiographic and fluoroscopic imaging for some time.¹⁹ Rather than modulating the beam properties at the source, a grid of lead leaves is fitted over the detector to preferentially absorb off-axis radiation not contributing to primary photon fluence. In CBCT systems, the lead leaves are arranged in a radial pattern centered on the focal spot of the FPD. Antiscatter grids have been evaluated in several experimental CBCT systems with mixed results.^8,16,19,20 A reduction in both cupping artifact and overall scatter has been observed,^8,16 though there may be insufficient improvement in contrast and observed image quality to warrant use except in situations of high scatter.^16,19 Siewerdsen et al¹⁶ evaluated antiscatter grids in a linear accelerator-coupled CBCT system and found that image quality and CNR improved only in situations of high scatter—such as with a large FOVz covering a large anatomic site—or in input quantum-limited situations such as with high dose or low spatial resolution. To the extent that antiscatter grids improve soft-tissue contrast and artifacts, they also increase noise, which leads to a degradation in overall image quality. An escalation in dose or reduction in spatial resolution is needed to offset the increased noise with the implementation of grids. For a relatively small FOVz, such as that used in a targeted head and neck scan, antiscatter grids may improve image contrast and reduce cupping artifacts, but the increased noise requires that the dose be increased or spatial resolution be decreased to produce a high-quality image with a favorable CNR.¹⁶

Scatter Correction Algorithms

Some sort of scatter subtraction or homogenization preprocessing algorithm is used in most clinical CBCT systems.^2,3,21 Several approaches have been studied, including Monte Carlo simulations, blocker-based or beam-stop techniques, analytic calculations, and collimator shadow estimation.^22–24 Perhaps the most theoretically robust algorithm is that based on the Monte Carlo simulation, which predicts scatter on the basis of a voxel density model of the entire acquired tissue volume during preprocessing.^22,25 The predicted scatter contribution at each detector element is then subtracted before reconstruction. Monte Carlo simulations still require significant computation time, however, which has fueled continued research in other algorithmic approaches. Methodologically, algorithms do not reduce the additional patient dose attributable to scatter, but they have been able to achieve significant improvements in image uniformity, CNR, and CT number accuracy.^22,25 They can, of course, be implemented in conjunction with other direct methods of scatter reduction.

Dynamic Range

Dynamic range, a quality of the detector, refers to the range of incident signal intensities that can be successfully captured and transmitted as image data. A large detector dynamic range generally corresponds to improved contrast resolution. Although the dynamic range of aSi:H FPDs exceeds that of x-ray intensifier/CCD detectors, it is still slightly inferior to the ceramic detectors used in MDCT.⁸ Solid state aSi:H FPDs are characterized by a dynamic range of ∼10⁴:1, digitized into a 14-bit readout, compared with ∼10⁶:1 for ceramic scintillation material in MDCT detectors.^26,27 To realize the full dynamic range potential of aSi:H FPDs, Roos et al²⁷ described an FPD with a dynamic gain-switching mode, effectively increasing the dynamic range by a factor of 6. Image acquisition in dynamic gain-switching mode extends the dynamic range to 16 bits and can enable contrast resolution of 3 Hounsfield units (HU), which rivals that of MDCT and exceeds the 5- to 10-HU low-contrast detectability typically quoted for current CBCT systems.^3,8,21

Temporal Resolution

Temporal resolution refers to the ability of an imaging system to discriminate sequentially acquired projection data separated by small time intervals. With higher temporal resolution, more projection datasets can be acquired over a fixed gantry rotation interval, thus improving contrast resolution. As it applies to contrast resolution, FPDs have inherently limited temporal resolution compared with the ceramic detectors used in MDCT systems.² Limited temporal resolution leads to image ghosting and “after-glow” or memory effects as well as streak artifacts, which degrade image quality and impair low-contrast detectability.²⁸

Limited temporal resolution at fixed gantry speeds in CBCT with FPD systems is related to the characteristics of the scintillator materials. CsI is a relatively slow scintillator susceptible to the after-glow effect, wherein the detector response to a new exposure is overwhelmed by the after-glow of the previous exposure, particularly if that exposure was transmitting high signal intensity such as with high-contrast structures.²⁹ This restricts the acquisition speed of the scanner in order that ghost images from after-glow can be minimized, thus placing a limit on gantry rotation speed and overall data-acquisition time. Subtracting a fraction of the previous image during preprocessing can help minimize this effect.⁸

Spatial Resolution

The spatial resolution of an imaging system is its ability to discriminate objects of different attenuation at small separation distances. It is typically described as the spatial frequency (measured in line pairs per centimeter [lp/cm]) that can be discriminated with a 10% detection of true contrast. The “modulation transfer function” (MTF) relates the percentage of actual contrast conferred to the spatial frequency of inserts in a phantom and is the product of the Fourier transform of a composite of functions describing image blur, unsharpness, and contrast response in reference to the ability to resolve line pairs per unit length. Spatial resolution is determined primarily by the inherent blurring in the detection apparatus and the individual area of the detection elements.²⁶ “Binning” refers to the process of grouping detector elements together for the transmission of 1 uniform signal; 1 × 1 binning affords the greatest ultimate spatial resolution but at the expense of the SNR if the dose is held constant. Improved SNR is possible with 2 × 2 and larger binning sizes. Superior spatial resolution is one of the most attractive qualities of CBCT imaging and is largely the result of FPD technology and isotropic data acquisition.

For images acquired at 125 kVp and reconstructed with a sharp kernel, the MiniCAT temporal bone protocol discriminates a spatial frequency of 14–16 lp/cm with 10% contrast detection (personal communication with Rohini Rebello-D'Souza, September 25, 2008). The MTF curves for images acquired under several MiniCAT protocols are depicted in Fig 6. Gupta et al⁸ have described spatial resolutions of 22–24 lp/cm in images acquired at 120 kVp with 2 × 2 binning of the detector elements in an FPD CBCT system as well. This spatial resolution corresponds to isometric voxels the size of a 200- to 250-μm cube. As mentioned under “Reconstruction Algorithms” above, isometric voxels as small as 150 × 150 × 150 μm³ at the isocenter have been achieved.

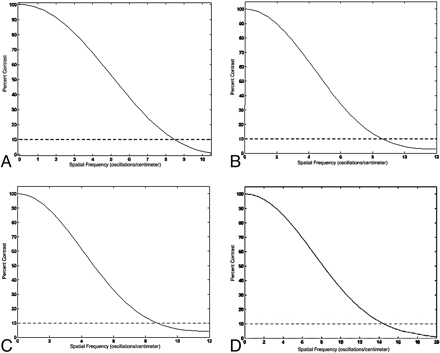Fig 6. MTF curves for 4 MiniCAT exposure protocols. MTF curves depict spatial frequency (line pairs per centimeter) as a function of true contrast detection. Spatial resolution is conventionally described as the spatial frequency that can be discriminated with a 10% detection of true contrast. A−D, The MiniCAT protocols: sinus 20s 600 (20 seconds, 600 frames), sinus 10s 300 (10 seconds, 300 frames), sinus 10s 150 (10 seconds, 150 frames), and temporal bone 20s 600 (20 seconds, 600 frames) respectively. Spatial resolution is 8–9 lp/cm for the sinus 20s (600) protocol and 14–16 lp/cm for the temporal bone 20s (600) protocol. Reprinted with permission of Xoran Technologies, Ann Arbor, Mich.

DQE

DQE is a useful metric for characterizing the overall efficiency of an x-ray imaging detector. It is calculated as the square of the input SNR divided by the square of the output SNR and represents the overall detector effectiveness in producing an image with high fidelity to the incident “data” provided during acquisition. DQE ranges from 0 to 1, whereas a detector that produces information content exactly congruent to that of the x-ray beam has a DQE of 1 (this is a hypothetic situation).

CsI aSi:H FPDs are indirect x-ray conversion systems that have DQEs in the range of 0.6–0.7, superior to their direct conversion amorphous selenium (aSe) FPD competitors, which are characterized by DQEs of approximately 0.35.²⁶ Bacher er al³⁰ have demonstrated the importance of superior DQE in aSi FPDs compared with aSe detectors in a study of digital chest radiographs. Lower DQE detectors afford lower dosing during image acquisition with equal or superior clinical quality and low-contrast detectability.^30–32

Although the introduction of high DQE indirect-conversion aSi:H FPDs into CBCT systems is a significant technical advancement, these detectors still have a slightly inferior DQE compared with the detectors traditionally used in MDCT systems.^8,33 This remains one of the technical challenges limiting low-contrast detectability in most CBCT systems.

Low-Contrast Detectability

Contrast resolution describes the ability of an imaging system to discriminate differences in tissue attenuation, as measured in HU. The low-contrast detectability in CBCT systems depends on both the dynamic range and temporal resolution of the detector as well as x-ray scatter and quantum noise.

CBCT systems under evaluation for head and neck imaging are typically described as having soft-tissue contrast discrimination of approximately 10 HU.^3,21 Modern MDCT scanners have contrast resolution approaching 1 HU. This limited contrast resolution remains a barrier to the extension of CBCT technologies into diagnostic imaging, in which detection of small changes in soft-tissue attenuation is a premium. Recent research has focused on scatter reduction and improvements in dynamic range and temporal resolution in an effort to improve contrast resolution without unnecessarily increasing patient dose. In fact, 3-HU discrimination has been achieved in experimental CBCT systems (see “Dynamic Range” subheading), though this has yet to translate to commercial scanners.⁸

Dose

The radiation-dose parameter in CT imaging is related foremost to patient safety, but it is also associated with image quality. In a simplistic model of conventional spiral CT, radiation dose increases proportionally with increased voltage (kVp) and tube current (milliampere [mA]) and can be decreased if the pixel size, section thickness, or pitch is increased. With other parameters held constant, increased radiation dose generally decreases quantum noise and affords improved contrast resolution. On the basis of the indication for imaging, exposure protocols are adapted to generate optimal image quality while delivering a justifiable dose to the patient.

An understanding of conventional CT dose measurement methodology is important to recognize the limitations confronting many CBCT dosimetry studies. By convention, the CT dose index (CTDI) and dose-length product (DLP), measured in grays (Gy), and the effective dose, measured in sieverts (Sv), are used to describe the radiation dose delivered during a CT scanning of the head or other anatomic region. Several variations on the CTDI parameter have been developed, primarily for the purposes of standardization and improved accuracy, with CTDI₁₀₀ being a common metric with defined integration limits used to describe the absorbed dose delivered during a single axial-section acquisition at particular exposure settings.³⁴ It is measured with a 100-mm ionization chamber implanted in a head or body phantom and is expressed as

where N is the number of tomographic sections imaged in a single rotation, T is the beam width, and D(z) is the dose profile function along the z-axis. The weighted CTDI (CTDI_w) is a more accurate reflection of the dose profile in the single-section FOV and is calculated as the weighted sum of central (CTDI_100c) and peripheral (CTDI_100p) CTDI₁₀₀s:

The DLP measures the total absorbed dose of a complete scan and is calculated by adding the CTDI_w of each section in the FOV_z and then multiplying by the section thickness. The effective dose estimates a patient's stochastic risk of developing late radiation effects given the anatomic distribution of the exposure. It is calculated by multiplying absorbed dose measurements by appropriate scalars on the basis of the anatomic and physiologic characteristics of the exposure field.

Conventional dosimetry metrics such as the CTDI_w cannot be directly adapted for CBCT imaging because of the altered beam geometry and scattered radiation profile of conebeam systems. Conventional ion-chamber inserts 10 cm in length do not absorb the entire expanded z-direction beam, which leads to a significant underestimation of delivered dose.^18,35,36 Attempts have been made to develop techniques that generate absorbed-dose metrics comparable with those used in conventional CT, such as the CTDI_w, but a standardized and universally applicable technique has yet to be adopted.^8,18,36 Viewed collectively, dosing studies of head and neck CBCT scans also have a lack of common exposure protocols and measurement methodologies, producing a wide range of results and making it difficult to draw coherent overall conclusions.⁸

Accurate dose evaluation is important for CBCT technology because these systems are often touted as low-dose alternatives to MDCT for applications such as sinus and temporal bone imaging, among others. Most dosimetry experiments suggest that the dose delivered during CBCT scans is lower than that in conventional MDCT for similar imaging studies, but it has been difficult to control the many variables affecting radiation dose. There is speculation that there may actually be little difference in absorbed dose measurements when FOVs and image quality parameters between CBCT and MDCT are approximated.^8,18,37

Commercial CBCT scanners designed for dedicated head and neck imaging have application-specific exposure parameter protocols, with FOVs designed to capture the area of interest and minimize exposure to adjacent structures. In the absence of a standardized absorbed dose metric comparable with the CTDI used in conventional CT, estimations of an effective dose for these scanners are often evaluated by point-dose measurements generated with thermoluminescent devices implanted into anthropomorphic head phantoms. In an experimental C-arm model, Daly et al³⁸ found the effective dose for a head and neck CBCT scan of 16-cm head phantoms to be 0.1–0.35 mSv, depending on whether exposure parameters were optimized for bony or soft-tissue resolution. For reference, the expected effective dose of a typical MDCT scan of the head is 1–2 mSv.³⁴ An effective dose for sinus imaging in commercial dedicated head and neck CBCT scanners has been estimated to be approximately 0.2 mSv.^39,40 Peltonen et al³⁷ described the effective dose for limited CBCT imaging of the middle ear to be 13 uSv, 60 times lower than that of a conventional MDCT scan of the temporal bone.

Comparisons of point-dose measurements have also been made for commercial dedicated dentomaxillofacial CBCT scanners, yielding effective dosing in the range of 13–498 μSv, most falling in the approximate range of 30–80 μSv, depending on scanning protocol, FOV, and manufacturer.^41–43